









| Definizione Geometrica | Rettangolo Aureo | Triangolo 72°,72°,36° | Triangolo 36°,36°,108° | Pentagono | Spirale |
DEFINIZIONE GEOMETRICA
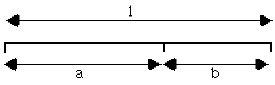 Ripartizione di un segmento in due parti, che
stanno tra loro come la maggiore (a) sta al segmento intero (1); utilizzando i simboli si
ha: 1:a=a:b.
Ripartizione di un segmento in due parti, che
stanno tra loro come la maggiore (a) sta al segmento intero (1); utilizzando i simboli si
ha: 1:a=a:b.
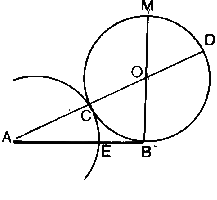 Se AB è il
segmento dato, si conduca la per perpendicolare ad AB nell’estremo B e si prenda su
di esso il segmento BO, metà di AB, indi col centro in O si descriva la circonferenza di
raggio OB, che risulterà tangente in B alla retta AB. Si unisca A con O e si chiamino C e
D le intersezioni della retta AO con la circonferenza; si porti infine su AB il segmento
AE congruente ad AC. Proveremo che AE è il segmento cercato, cioè che sussiste la
proporzione:
Se AB è il
segmento dato, si conduca la per perpendicolare ad AB nell’estremo B e si prenda su
di esso il segmento BO, metà di AB, indi col centro in O si descriva la circonferenza di
raggio OB, che risulterà tangente in B alla retta AB. Si unisca A con O e si chiamino C e
D le intersezioni della retta AO con la circonferenza; si porti infine su AB il segmento
AE congruente ad AC. Proveremo che AE è il segmento cercato, cioè che sussiste la
proporzione:
AB : AE = AE : EB
Infatti per il teorema della secante e della tangente (se da un punto si conducono ad una circonferenza una secante e una tangente, il segmento determinato dalla circonferenza sulla tangente è medio proporzionale fra i segmenti determinati sulla secante e aventi un estremo in quel punto) si ha:
AD : AB = AB : AC
Da cui scomponendo si ottiene:
(AD – AB) : AB = (AB – AC) : AC
Ma siccome AB è congruente a CD e AC è congruente ad AE si ha pure:
AD – AB = AD – CD = AC = AE
AB – AC = AB – AE =EB
Perciò l’ultima proporzione diventa:
AE : AB = EB : AE
Da cui invertendo:
AB : AE = AE : EB
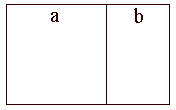
Esiste uno speciale rettangolo le cui proporzioni corrispondono alla sezione aurea. Il suo nome è rettangolo aureo. Per costruire il rettangolo aureo si disegni un quadrato di lato a i cui vertici chiameremo, a partire dal vertice in alto a sinistra e procedendo in senso orario, AEFD. Quindi dividere il segmento AE in due chiamando il punto medio A'. Utilizzando il compasso e puntando in A' disegnare un arco che da F intersechi il prolungamento del segmento AE in B. Con una squadra disegnare il segmento BC perpendicolare ad AB. Il rettangolo ABCD è un rettangolo aureo nel quale Ab è diviso dal punto E esattamente nella sezione aurea:
AE:AB=EB:AE
TRIANGOLO CON ANGOLI DI MISURA: 72°, 72°, 36°.
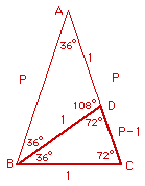 Dato un triangolo
isoscele i cui angoli alla base misurano 72° ciascuno, e l’angolo al vertice misura
36°, la bisettrice di un angolo alla base divide il lato obliquo opposto nel punto
d’intersezione in due segmenti in modo tale da creare una sezione aurea. Infatti il
triangolo ABC è simile al triangolo BCD. E da questo risulta che:
Dato un triangolo
isoscele i cui angoli alla base misurano 72° ciascuno, e l’angolo al vertice misura
36°, la bisettrice di un angolo alla base divide il lato obliquo opposto nel punto
d’intersezione in due segmenti in modo tale da creare una sezione aurea. Infatti il
triangolo ABC è simile al triangolo BCD. E da questo risulta che:
AC:BC=BD:DC
e dunque:
AC:AD=AD:DC
TRIANGOLO CON ANGOLI DI MISURA: 36°, 36°, 108°.
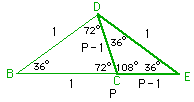 Dato un triangolo isoscele i cui
angoli alla base misurano 36° ciascuno, e l’angolo al vertice misura 108°, il lato
obliquo e la differenza tra la base e il lato obliquo danno vita a una sezione aurea.
Infatti il triangolo CDE è simile al triangolo ABD della figura precedente.
Dato un triangolo isoscele i cui
angoli alla base misurano 36° ciascuno, e l’angolo al vertice misura 108°, il lato
obliquo e la differenza tra la base e il lato obliquo danno vita a una sezione aurea.
Infatti il triangolo CDE è simile al triangolo ABD della figura precedente.
PENTAGONO E TRIANGOLI IN ESSO CONTENUTI
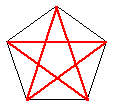 All’interno di un
pentagono, ogni lato forma con due diagonali (il segmento che unisce due punti non
adiacenti) un triangolo dagli angoli con misura 72°, 72°, 36°, con le proprietà
spiegate in precedenza. Ogni lato forma, con il punto d’incontro di due diagonali
consecutive, un triangolo dagli angoli 36°, 36°, 108°, con le proprietà descritte in
precedenza. Cioè il lato del pentagono regolare è la sezione aurea di una sua diagonale
e il punto d' intersezione tra due diagonali divide ciascuna di esse in due segmenti che
stanno nel rapporto aureo.
All’interno di un
pentagono, ogni lato forma con due diagonali (il segmento che unisce due punti non
adiacenti) un triangolo dagli angoli con misura 72°, 72°, 36°, con le proprietà
spiegate in precedenza. Ogni lato forma, con il punto d’incontro di due diagonali
consecutive, un triangolo dagli angoli 36°, 36°, 108°, con le proprietà descritte in
precedenza. Cioè il lato del pentagono regolare è la sezione aurea di una sua diagonale
e il punto d' intersezione tra due diagonali divide ciascuna di esse in due segmenti che
stanno nel rapporto aureo.
SPIRALE AUREA
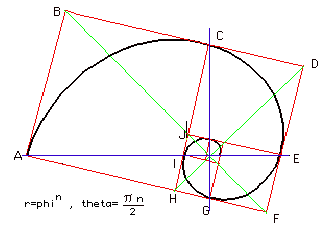
Se all’interno di un rettangolo aureo si disegna un quadrato con lato uguale al lato
minore del rettangolo, il rettangolo differenza sarà anch’esso un rettangolo aureo.
Si ripeta l’operazione per almeno cinque volte al fine di avere un effetto visivo
adeguato. Si punti la punta del compasso sul vertice del quadrato che giace sul lato lungo
del rettangolo e si tracci l’arco che unisce i gli estremi dei due lati che formano
l'angolo scelto. Si ripete l'operazione per ogni quadrato disegnato in modo da creare una
linea continua.

